Al contrario, nel caso di una combinazione, l'ordine non ha alcuna importanza. Non solo in matematica, ma anche nella vita pratica, continuiamo con questi due concetti regolarmente. Anche se non lo notiamo mai. Quindi, leggere attentamente l'articolo per sapere in che modo questi due concetti sono diversi.
Grafico comparativo
| Base per il confronto | Permutazione | Combinazione |
|---|---|---|
| Senso | La permutazione si riferisce ai diversi modi di organizzare un insieme di oggetti in un ordine sequenziale. | La combinazione si riferisce a diversi modi di scegliere gli elementi da una vasta serie di oggetti, in modo che il loro ordine non contenga. |
| Ordine | pertinente | non pertinente |
| denota | Preparativi | Selezione |
| Che cos'è? | Elementi ordinati | Insiemi non ordinati |
| risposte | Quanti diversi arrangiamenti possono essere creati da un determinato insieme di oggetti? | Quanti gruppi diversi possono essere scelti da un gruppo più ampio di oggetti? |
| Derivazione | Permutazione multipla da una singola combinazione. | Singola combinazione da una singola permutazione. |
Definizione di permutazione
Definiamo la permutazione come modi diversi di organizzare alcuni o tutti i membri di un insieme in un ordine specifico. Implica tutto il possibile arrangiamento o riorganizzazione del set dato, in ordine distinguibile.
Ad esempio, Tutte le permutazioni possibili create con lettere x, y, z -
- Prendendo tutti e tre alla volta sono xyz, xzy, yxz, yzx, zxy, zyx.
- Prendendo due alla volta sono xy, xz, yx, yz, zx, zy.
Il numero totale di permutazioni possibili di n cose, prese alla volta, può essere calcolato come:
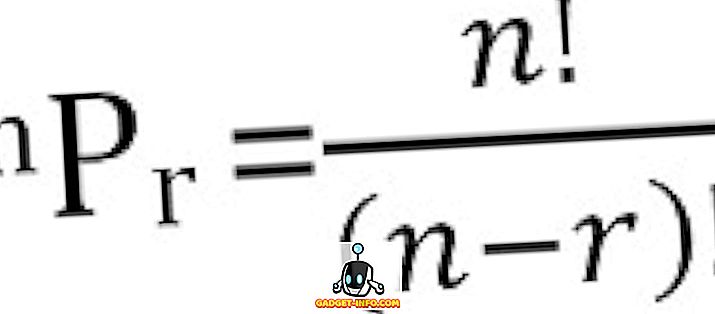
Definizione di combinazione
La combinazione è definita come i diversi modi, di selezionare un gruppo, prendendo alcuni o tutti i membri di un set, senza il seguente ordine.
Ad esempio, tutte le possibili combinazioni scelte con la lettera m, n, o -
- Quando tre o tre lettere devono essere selezionate, l'unica combinazione è mno
- Quando due o tre lettere devono essere selezionate, le combinazioni possibili sono mn, no, om.
Il numero totale di combinazioni possibili di n cose, prese alla volta può essere calcolato come:
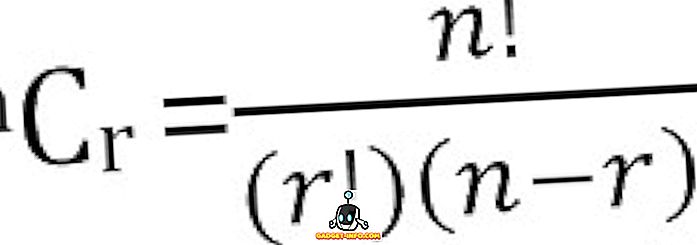
Differenze chiave tra permutazione e combinazione
Le differenze tra permutazione e combinazione sono tracciate chiaramente per i seguenti motivi:
- Il termine permutazione si riferisce a diversi modi di organizzare un insieme di oggetti in un ordine sequenziale. La combinazione implica diversi modi di scegliere gli elementi da un grande insieme di oggetti, in modo tale che il loro ordine sia irrilevante.
- Il principale punto di distinzione tra questi due concetti matematici è l'ordine, il posizionamento e la posizione, cioè le caratteristiche di permutazione sopra menzionate sono importanti, il che non importa nel caso della combinazione.
- La permutazione denota diversi modi per sistemare cose, persone, cifre, alfabeti, colori, ecc. D'altra parte, la combinazione indica diversi modi di selezionare voci di menu, cibo, vestiti, soggetti, ecc.
- La permutazione non è altro che una combinazione ordinata mentre la combinazione implica insiemi non ordinati o abbinamento di valori all'interno di criteri specifici.
- Molte permutazioni possono essere derivate da una singola combinazione. Viceversa, solo una singola combinazione può essere ottenuta da una singola permutazione.
- Permutazione risponde Quanti accordi diversi possono essere creati da un dato insieme di oggetti? Al contrario della combinazione che spiega Quanti gruppi diversi possono essere scelti da un gruppo più ampio di oggetti?
Esempio
Supponiamo, vi sia una situazione in cui devi scoprire il numero totale di possibili campioni di due su tre oggetti A, B, C. In questa domanda, prima di tutto, devi capire se la domanda è correlata alla permutazione o combinazione e l'unico modo per scoprirlo è verificare se l'ordine è importante o meno.
Se l'ordine è significativo, la domanda è relativa alla permutazione, e i possibili campioni saranno, AB, BA, BC, CB, AC, CA. Dove, AB è diverso da BA, BC è diverso da CB e AC è diverso CA.
Se l'ordine è irrilevante, la domanda è relativa alla combinazione e i possibili campioni saranno AB, BC e CA.
Conclusione
Con la discussione di cui sopra, è chiaro che permutazione e combinazione sono termini diversi, che sono usati in matematica, statistica, ricerca e la nostra vita quotidiana. Un punto da ricordare, riguardo questi due concetti è che, per un dato insieme di oggetti, la permutazione sarà sempre più alta della sua combinazione.