La differenza tra correlazione e regressione è una delle domande più frequenti nelle interviste. Inoltre, molte persone soffrono di ambiguità nella comprensione di questi due. Quindi, prendi una lettura completa di questo articolo per avere una chiara comprensione di questi due.
Grafico comparativo
| Base per il confronto | Correlazione | Regressione |
|---|---|---|
| Senso | La correlazione è una misura statistica che determina la co-relazione o l'associazione di due variabili. | La regressione descrive come una variabile indipendente è numericamente correlata alla variabile dipendente. |
| uso | Per rappresentare la relazione lineare tra due variabili. | Per adattare una linea migliore e stimare una variabile sulla base di un'altra variabile. |
| Variabili dipendenti e indipendenti | Nessuna differenza | Entrambe le variabili sono diverse. |
| Indica | Il coefficiente di correlazione indica la misura in cui due variabili si muovono insieme. | La regressione indica l'impatto di una variazione di unità nella variabile conosciuta (x) sulla variabile stimata (y). |
| Obbiettivo | Trovare un valore numerico che esprima la relazione tra le variabili. | Valutare i valori della variabile casuale sulla base dei valori della variabile fissa. |
Definizione di correlazione
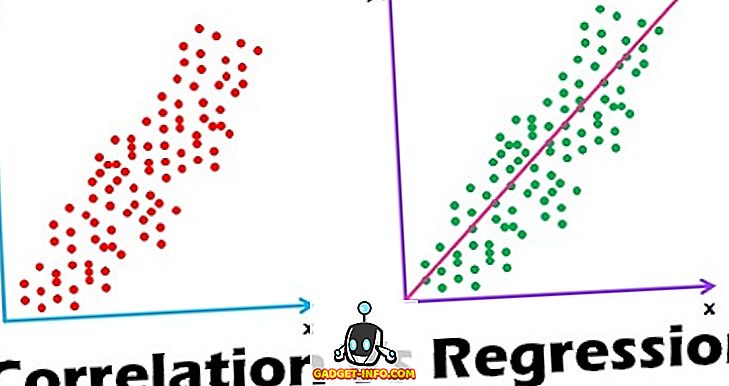
Il termine correlazione è una combinazione di due parole "Co" (insieme) e relazione (connessione) tra due quantità. La correlazione è quando, al momento dello studio di due variabili, si osserva che una variazione di unità in una variabile è ritmata da una variazione equivalente in un'altra variabile, cioè diretta o indiretta. Oppure si dice che le variabili non sono correlate quando il movimento in una variabile non corrisponde a nessun movimento in un'altra variabile in una direzione specifica. È una tecnica statistica che rappresenta la forza della connessione tra coppie di variabili.
La correlazione può essere positiva o negativa. Quando le due variabili si muovono nella stessa direzione, cioè un aumento di una variabile risulterà nel corrispondente aumento di un'altra variabile e viceversa, le variabili verranno considerate positivamente correlate. Ad esempio : profitto e investimento.
Al contrario, quando le due variabili si muovono in direzioni diverse, in modo tale che un aumento di una variabile determinerà una diminuzione di un'altra variabile e viceversa, questa situazione è nota come correlazione negativa. Ad esempio : prezzo e domanda di un prodotto.
Le misure di correlazione sono date come sotto:
- Coefficiente di correlazione momento prodotto di Karl Pearson
- Il coefficiente di correlazione di ranghi di Spearman
- Diagramma di dispersione
- Coefficiente di deviazioni concomitanti
Definizione di regressione
Una tecnica statistica per stimare la variazione della variabile dipendente dalla metrica dovuta alla variazione di una o più variabili indipendenti, basata sulla relazione matematica media tra due o più variabili è nota come regressione. Svolge un ruolo significativo in molte attività umane, in quanto è uno strumento potente e flessibile che consente di prevedere eventi passati, presenti o futuri sulla base di eventi passati o presenti. Ad esempio : sulla base delle registrazioni passate, è possibile stimare il profitto futuro di un'azienda.
In una regressione lineare semplice, ci sono due variabili x e y, in cui y dipende da x o say influenzato da x. Qui y è chiamato come dipendente, o variabile di criterio e x è indipendente o variabile predittore. La linea di regressione di y su x è espressa come sotto:
y = a + bx
dove, a = costante,
b = coefficiente di regressione,
In questa equazione, aeb sono i due parametri di regressione.
Differenze chiave tra correlazione e regressione
I punti indicati di seguito, spiegano in dettaglio la differenza tra correlazione e regressione:
- Una misura statistica che determina la correlazione o l'associazione di due quantità è nota come correlazione. La regressione descrive come una variabile indipendente è numericamente correlata alla variabile dipendente.
- La correlazione viene utilizzata per rappresentare la relazione lineare tra due variabili. Al contrario, la regressione viene utilizzata per adattare la linea migliore e stimare una variabile sulla base di un'altra variabile.
- In correlazione, non c'è differenza tra variabili dipendenti e indipendenti, cioè la correlazione tra x e y è simile a y e x. Viceversa, la regressione di y su x è diversa da x su y.
- La correlazione indica la forza dell'associazione tra le variabili. Al contrario, la regressione riflette l'impatto della variazione di unità nella variabile indipendente sulla variabile dipendente.
- La correlazione mira a trovare un valore numerico che esprima la relazione tra le variabili. A differenza della regressione il cui obiettivo è predire i valori della variabile casuale sulla base dei valori della variabile fissa.
Conclusione
Con la discussione di cui sopra, è evidente che c'è una grande differenza tra questi due concetti matematici, sebbene questi due siano studiati insieme. La correlazione viene utilizzata quando il ricercatore vuole sapere se le variabili in studio sono correlate o meno, se sì allora qual è la forza della loro associazione. Il coefficiente di correlazione di Pearson è considerato la migliore misura di correlazione. Nell'analisi di regressione, viene stabilita una relazione funzionale tra due variabili in modo da rendere future proiezioni sugli eventi.